Iki iletken arasina bir yalitkan koyarak yuk depolayan elektrik eleamnlarina kondansator ve bunu yapabilme ozelligine siga yada kapasitans denir.
Genel olarak parelel plaka kapasitorleri mevcut olsa da farkli cesitleri mevcuttur. Yukleme islemi yukler esitlendiginde durur.Basit olarak kapasitor formulu
q=CV dir.
ayrica: q=EAε0 DIR
Silindirsel Kondansator
Silindirsel kondansatörler iki metal silindir tabakanın birbirinin içine yerleştirilmesi ve aralarına yalıtkan bir malzemenin koyulmasıyla tasarlanır. Bu tip kondansatörlerin günlük hayatta kullanımı çoktur. Kablolar, yüksek gerilim havai hatları veya geçit izalatörleri bu kullanım alanlarına örnek olarak verilebilir.[kaynak belirtilmeli] Benzetim açısından da kolaylık sağlayan silindirsel kondansatörlerin incelenmesinde eşmerkezli olanları kullanılır.
İç silindir yarıçapı  , dış silindir yarıçapı
, dış silindir yarıçapı  iken, silindir uzunlukları
iken, silindir uzunlukları  olarak alınır. Gerilim iç silindire uygulanır, dış silindir ise gerilimsiz bırakılır. Bu durumda sistem yalıtkan malzeme üzerinde yük depolar. Kapasite değeri ise aşağıdaki gibi bulunur.
olarak alınır. Gerilim iç silindire uygulanır, dış silindir ise gerilimsiz bırakılır. Bu durumda sistem yalıtkan malzeme üzerinde yük depolar. Kapasite değeri ise aşağıdaki gibi bulunur.
 , dış silindir yarıçapı
, dış silindir yarıçapı  iken, silindir uzunlukları
iken, silindir uzunlukları  olarak alınır. Gerilim iç silindire uygulanır, dış silindir ise gerilimsiz bırakılır. Bu durumda sistem yalıtkan malzeme üzerinde yük depolar. Kapasite değeri ise aşağıdaki gibi bulunur.
olarak alınır. Gerilim iç silindire uygulanır, dış silindir ise gerilimsiz bırakılır. Bu durumda sistem yalıtkan malzeme üzerinde yük depolar. Kapasite değeri ise aşağıdaki gibi bulunur. |
Kuresel kondansator
Küresel kondansatörler iki metal kürenin iç içe konulup, aralarına bir yalıtkanın yerleştirilmesiyle oluşturulur. Gündelik hayatta fazla kullanım alanı yoktur, ancak özellikle yüksek gerilim tekniğinde benzetim yapmak için kullanılır ve kolaylık sağlar. Farklı çeşitleri mevcuttur. Kürelerin merkezleri birbirinden ayrık ve küreler birbiriyle ilişkisiz olabilir. Ancak hesaplamada kolaylık olması açısından eş merkezli küresel kondansatörler kullanılacaktır.
İç küre yarıçapının  , dış küre yarıçapının
, dış küre yarıçapının  olduğu kabul edilir. Kondansatör
olduğu kabul edilir. Kondansatör 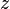 ekseninde ise yine
ekseninde ise yine  ve
ve  uzaklıkları arasında yer alır. İç küreye gerilim uygulanıp, dış küreye gerilim uygulanmadığında, sistem belli bir değerde yük depolama özelliğine sahip olur. Eş merkezli küresel kondansatörlerde kapasite değerinin ifadesi aşağıdaki gibi yazılabilir.
uzaklıkları arasında yer alır. İç küreye gerilim uygulanıp, dış küreye gerilim uygulanmadığında, sistem belli bir değerde yük depolama özelliğine sahip olur. Eş merkezli küresel kondansatörlerde kapasite değerinin ifadesi aşağıdaki gibi yazılabilir.
 , dış küre yarıçapının
, dış küre yarıçapının  olduğu kabul edilir. Kondansatör
olduğu kabul edilir. Kondansatör 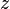 ekseninde ise yine
ekseninde ise yine  ve
ve  uzaklıkları arasında yer alır. İç küreye gerilim uygulanıp, dış küreye gerilim uygulanmadığında, sistem belli bir değerde yük depolama özelliğine sahip olur. Eş merkezli küresel kondansatörlerde kapasite değerinin ifadesi aşağıdaki gibi yazılabilir.
uzaklıkları arasında yer alır. İç küreye gerilim uygulanıp, dış küreye gerilim uygulanmadığında, sistem belli bir değerde yük depolama özelliğine sahip olur. Eş merkezli küresel kondansatörlerde kapasite değerinin ifadesi aşağıdaki gibi yazılabilir. |
Bu ifadede kesin olan tek şey, aradaki malzemenin dielektrik katsayısının kapasite değerini doğru orantılı etkilediğidir.  ve
ve  yarıçapları ise alacakları değerlere göre kapasite değerini etkilerler, bu oran tasarım açısından çeşitlilik olanağı sunar.
yarıçapları ise alacakları değerlere göre kapasite değerini etkilerler, bu oran tasarım açısından çeşitlilik olanağı sunar.
 ve
ve  yarıçapları ise alacakları değerlere göre kapasite değerini etkilerler, bu oran tasarım açısından çeşitlilik olanağı sunar.
yarıçapları ise alacakları değerlere göre kapasite değerini etkilerler, bu oran tasarım açısından çeşitlilik olanağı sunar.Yüklü Bir Kondansatörün Enerjisi
Bir kondansatörü yüklerken, alçak potansiyeldeki levhalardan yüksek potansiyeldeki levhaya yük taşınmaktadır. Bunun için ise elektriksel kuvvetlere karşı bir iş yapmak gerekmektedir.
Başlangıçta yüksüz olan levhalar arasındaki potansiyel farkı sıfırdır. Kondansatör yüklenip q kadar yük taşıdıktan sonra, levhalar arasındaki potansiyel farkı V değerine ulaşır.
Burada, q = C.V bağıntısı vardır. Daha önceki bağıntıyı düzenlersek bu bağıntıyı rahatlıkla elde edebiliriz. Bu bağıntıdan anlaşıldığı gibi q arttıkça V artar. Yani iki değer doğru orantılıdır. Doğru orantılı q - V grafiğinin altında kalan alan yapılan işi, dolayısıyla da depolanan enerjiyi verir.;
E = q.V/2 grafikte alanı veren bağıntıdır. Burada q yerine C.V yazarsak E = 1/2.C.V2 bağıntısını elde ederiz.
Burada,
E: Kondansatörde depolanan enerji (joule)
C: Kondansatörün sığası (farad)
V: Kondansatörün uçları arasındaki potansiyel farkı (volt)
Kondansatörler DC gerilimde (doğru gerilim)dolup boşalma yöntemiyle çalışır. Tam dolduğunda açık devre gibi davranır. Yani akım sıfır olur.
AC gerilim (alternatif gerilim) uygulandığında ise direnç gibi davranır. Bu direncin değeri gerilimin frekansına ve kondansatörün sığasına bağlıdır. Frekans arttıkça direnç azalır, frekans azaldıkça direnç artar.
Kondansatörlerin Bağlanması
Seri bağlama ve özellikleri
İki ya da daha fazla kondansatörün aynı yük kolu üzerinde olacak biçimde bağlanmasına seri bağlama denir.
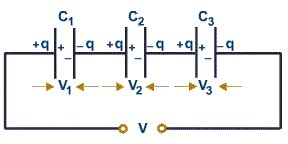
Şekildeki devrede sistemin iki ucu arasına V potansiyel farkı uygulanırsa, C1 sığalı kondansatör +q yükü ile yüklenir. Bu +q yükü C2 sığalı kondansatörden -q kadar yük çeker ve C2 sığalı kondansatör +q kadar yükle yüklenir. Bu da C3 sığalı kondansatöründen -q kadar yük çekerek onun da + q yükü ile yüklenmesine neden olur.
Böylece C, ve C3 sığalı kondansatörlerin en dıştaki levhalar üreteçten yüklenmiş, diğer levhalar ise etki ile yüklenmiş olur.
Buna göre seri bağlı kondansatörlerin sığaları ne olursa olsun her birinin yük miktarı eşittir. Toplam yük ise kondansatörlerden birinin yüküne eşittir.
Aynı potansiyel farkı altında, toplam yük kadar yük depolayan sığaya eşdeğer sığa denir.
Özellikler
- Her bir kondansatörün yükleri eşit ve toplam yük birinin yüküne eşittir. qT = q1 = q2 =q3
- Üç kondansatörün uçları arasındaki V potansiyel farkı, her bir kondansatörün uçları arasındaki potansiyel farklarının toplamına eşittir. V = V1 + V2 + V3
- Devrenin eşdeğer sığasının tersi, sığaların terslerinin toplamına eşittir. Eşdeğer sığa, 1/Ceş = 1/C1 + 1/C2 + 1/C3 bağıntısıyla bulunur.
- Eğer sığaları C1 ve C2 olan iki kondansatör seri bağlanmış ise eşdeğer sığa, Ceş = C1.C2/(C1 + C2) bağıntısıyla bulunur.
Bu şekilde ikişerli eşdeğer sığa bulmak işlem kolaylığı sağlar.
Seri bağlı ve sığaları eşit n tane kondansatör seri olarak bağlanırsa devrenin eşdeğer sığası, bir kondansatörün sığasının, kondansatör sayısına bölümünden bulunur. Ceş = C/n
Seri bağlı kondansatörlerin eşdeğer sığasının değeri, en küçük sığanın değerinden daha küçüktür. Örneğin 20 μF, 10 μF ve 1μF sığalı ve seri bağlı üç kondansatörün sığası en küçük sığa olan 1μF'dan daha küçüktür.
Paralel bağlama ve özellikleri
İki ya da daha fazla kondansatörün birer uçları bir noktaya bağlanarak elde edilen bağlama şekline paralel bağlamadenir.
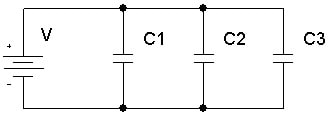
Paralel bağlı kondansatörlere V gerilimi uygulanırsa bütün kondansatörlerin gerilimi de yine V olur. Üretecin (+) kutbuna bağlı tarafı pozitif yüklü, (-) kutbuna bağlı tarafı ise negatif yükle yüklenir.
Özellikler
- Her bir kondansatörün uçları aynı noktalara bağlandığı için uçları arasındaki gerilimler aynı olur. V = V1 = V2 = V3
- Kondansatörlerin uçları arasındaki gerilimler eşitken sığalar farklı olduğu için yükler de farklı olur. Bu yüklerin toplamı toplam yüke eşittir. qT = q1 + q2 + q3
- Eşdeğer sığaların toplamı toplam sığayı verir. Buna göre eşdeğer sığa, Ceş = C1 + C2 + C3 bağıntısı ile bulunur.
Bildigimiz uzere bir kondansator icin iki adet iletken arasina yalitkan bir madde gereklidir.
Kondansatorun sigasini belirlemek icin gereken verilerden biri de de dielektrik katsayisidir.Bu katsayi her madde icin farklidir.Sigasi buyuk olan kondansatorun katsayisi da buyuk olmalidir.
Bir yukun olusturdugu yalitkanin icindeki elektrik alan
E=1/(4kε0 ). q/r.r dir.
). q/r.r dir.
 ). q/r.r dir.
). q/r.r dir.
u=1/2 ε0 E^2 Dir.
Hiç yorum yok:
Yorum Gönder